Nicômaco nasceu aproximadamente no ano 60, em Gerasa, era um dos principais membros da Escola Pitagórica e veio a falecer aproximadamente no ano 120.
Geralmente a aritmética grega estava mais ligada à filosofia do que com o que chamamos de matemática e talvez por isso teve um importante papel no neoplatonismo durante a Segunda Idade Alexandrina (período entre a primeira e a Segunda guerra púnica, em que os romanos se achavam em contato com os gregos intervindo em sua política interna). Era em Alexandria, na Universidade, que se encontrava o mais importante centro intelectual de todo o império.
É uma obra que contém apenas dois livros e o texto que chegou até nós talvez seja uma versão abreviada da obra original. Nela estudam-se as propriedades e as divisões dos números segundo os métodos e idéias dos Pitagóricos e Platônicos. Pode ter sido o primeiro trabalho que tratou a aritmética como um tópico separado da geometria.
Nicômaco não era muito habilidoso com a matemática, portanto ocupava-se apenas com as propriedades elementares dos números. Para ele os números tinham qualidades, eram melhores ou piores, mais jovens ou mais velhos.
No Livro I é feita uma classificação dos números. Primeiramente são classificados em pares e ímpares, depois em parmente pares ( potências de dois ), parmente ímpares (
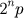
, onde p é ímpar p>1 e n>1 ) e imparmente pares ( 2p, onde p é ímpar e p>1 ). Os
números primos e compostos números perfeitos são definidos, é dada uma lista dos quatro primeiros números perfeitos ( 6, 28, 496, 8128 ) e uma descrição do crivo de Eratóstenes para obter números primos.
O Livro II contém um tratamento extenso dos
números figurados em duas e três dimensões.
Assim como outros escritores, ele considerava os números um e dois como geradores do sistema numérico, portanto o primeiro número "verdadeiro" era o três.
A Introdução à Aritmética contém erros bastante elementares, pois Nicômaco não dava provas dos resultados. Algumas vezes enunciou resultados que na verdade são falsos, baseado em exemplos numéricos como evidência.
Uma mostra deste tipo de erro é quando fala que o enésimo número perfeito tem n dígitos, e que eles terminam alternadamente em 6 e 8. Estas afirmações são meramente falsas e foram declaradas sem provas, pois eram conhecidos apenas quatro dos números perfeitos (6, 28, 496, 8128).
O quinto número perfeito é 8191 que não tem cinco dígitos como tinha anunciado Nicômaco e não termina em 6 ou 8.
Porém sua obra contém um teorema moderadamente sofisticado. Nicômaco observou que se os inteiros ímpares são agrupados segundo o esquema 1; 3+5; 7+9+11; 13+15+17+19; se obtém sucessivamente os cubos dos inteiros, por exemplo:
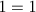
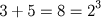
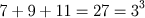
Isto, junto com a antiga observação pitagórica de que a soma dos n primeiros ímpares é igual a
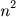
, leva à conclusão que a soma dos n primeiros cubos perfeitos é igual ao quadrado da soma dos n primeiros inteiros.




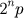 , onde p é ímpar p>1 e n>1 ) e imparmente pares ( 2p, onde p é ímpar e p>1 ). Os números primos e compostos números perfeitos são definidos, é dada uma lista dos quatro primeiros números perfeitos ( 6, 28, 496, 8128 ) e uma descrição do crivo de Eratóstenes para obter números primos.
O Livro II contém um tratamento extenso dos números figurados em duas e três dimensões.
Assim como outros escritores, ele considerava os números um e dois como geradores do sistema numérico, portanto o primeiro número "verdadeiro" era o três.
A Introdução à Aritmética contém erros bastante elementares, pois Nicômaco não dava provas dos resultados. Algumas vezes enunciou resultados que na verdade são falsos, baseado em exemplos numéricos como evidência.
Uma mostra deste tipo de erro é quando fala que o enésimo número perfeito tem n dígitos, e que eles terminam alternadamente em 6 e 8. Estas afirmações são meramente falsas e foram declaradas sem provas, pois eram conhecidos apenas quatro dos números perfeitos (6, 28, 496, 8128).
O quinto número perfeito é 8191 que não tem cinco dígitos como tinha anunciado Nicômaco e não termina em 6 ou 8.
Porém sua obra contém um teorema moderadamente sofisticado. Nicômaco observou que se os inteiros ímpares são agrupados segundo o esquema 1; 3+5; 7+9+11; 13+15+17+19; se obtém sucessivamente os cubos dos inteiros, por exemplo:
, onde p é ímpar p>1 e n>1 ) e imparmente pares ( 2p, onde p é ímpar e p>1 ). Os números primos e compostos números perfeitos são definidos, é dada uma lista dos quatro primeiros números perfeitos ( 6, 28, 496, 8128 ) e uma descrição do crivo de Eratóstenes para obter números primos.
O Livro II contém um tratamento extenso dos números figurados em duas e três dimensões.
Assim como outros escritores, ele considerava os números um e dois como geradores do sistema numérico, portanto o primeiro número "verdadeiro" era o três.
A Introdução à Aritmética contém erros bastante elementares, pois Nicômaco não dava provas dos resultados. Algumas vezes enunciou resultados que na verdade são falsos, baseado em exemplos numéricos como evidência.
Uma mostra deste tipo de erro é quando fala que o enésimo número perfeito tem n dígitos, e que eles terminam alternadamente em 6 e 8. Estas afirmações são meramente falsas e foram declaradas sem provas, pois eram conhecidos apenas quatro dos números perfeitos (6, 28, 496, 8128).
O quinto número perfeito é 8191 que não tem cinco dígitos como tinha anunciado Nicômaco e não termina em 6 ou 8.
Porém sua obra contém um teorema moderadamente sofisticado. Nicômaco observou que se os inteiros ímpares são agrupados segundo o esquema 1; 3+5; 7+9+11; 13+15+17+19; se obtém sucessivamente os cubos dos inteiros, por exemplo:
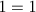
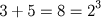
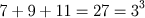
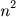 , leva à conclusão que a soma dos n primeiros cubos perfeitos é igual ao quadrado da soma dos n primeiros inteiros.
, leva à conclusão que a soma dos n primeiros cubos perfeitos é igual ao quadrado da soma dos n primeiros inteiros.