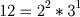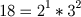Alterado em: 22/02/2008, 28/01/2003, 13/09/2000
Texto de: Valéria Ostete Jannis Luchetta; supervisão e orientação:
prof. Doutor Francisco César Polcino Milies; revisão LOB
Bibliografia:
- Polcino, César M. & Coelho, Sonia P., Números - Uma Introdução à Matemática, EDUSP, São Paulo, 1999.