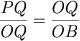Dentre os três problemas clássicos da antigüidade, talvez o problema de
quadrar um círculo seja o mais famoso.
Este problema consistia em encontrar um quadrado de tal forma que a sua área fosse igual à área de um círculo dado.
Ele deveria ser resolvido com régua e compasso (euclideanos), porém assim como na
trissecção de um ângulo e na
duplicação de um cubo isto não é possível.
No
Papiro Rhind ou Ahmes é dado uma solução plana para se construir um quadrado de área próxima a de um círculo.
Para isso o lado do quadrado deveria ser

do diâmetro do círculo. Embora esta não seja uma construção geométrica
precisa é uma boa aproximação, pois corresponde a tomar
3,1605 como valor para
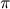
ao invés de
3m14159....
Porém os gregos antigos também tentaram achar outras soluções, através de algumas curvas que foram inventadas, ou através de construções mecânicas.
Anaxágoras foi o primeiro matemático do qual temos registro de ter tentado solucionar este problema.
Dinostratos desenvolveu um método para quadrar o círculo através de
quadratriz ou trissectriz de Hipias.
A
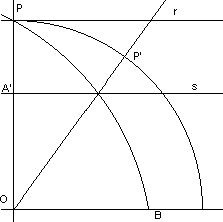
quadratriz de Hipias consiste em uma curva mecânica, que pode ser obtida da seguinte maneira:
dada a figura abaixo, suponha o raio OP se deslocando uniformemente até a posição OQ e ao mesmo tempo a reta r se deslocando
até OQ, também uniformemente. Depois de um tempo OP estará na posição OP' e r estará em s, cuja intersecção é o ponto A.
Assim a quadratriz é a curva descrita por A durante todo o percurso.
Quando Dinostrato observou uma notável propriedade da trissectriz de Hipias, a quadratura tornou-se uma questão simples. Ele descobriu que o arco PQ esta para o raio OQ assim como este raio esta para o segmento OB.
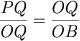 Através de uma construção geométrica podemos traçar um segmento b de comprimento igual ao do arco PQ. O retângulo de lados 2b e a (a=OQ) tem a área igual ao do círculo dado (círculo de raio a). E a partir desse retângulo facilmente constrói-se um quadrado que tenha a mesma área, assim conseguimos quadrar o círculo.
Através de uma construção geométrica podemos traçar um segmento b de comprimento igual ao do arco PQ. O retângulo de lados 2b e a (a=OQ) tem a área igual ao do círculo dado (círculo de raio a). E a partir desse retângulo facilmente constrói-se um quadrado que tenha a mesma área, assim conseguimos quadrar o círculo.




 do diâmetro do círculo. Embora esta não seja uma construção geométrica
precisa é uma boa aproximação, pois corresponde a tomar 3,1605 como valor para
do diâmetro do círculo. Embora esta não seja uma construção geométrica
precisa é uma boa aproximação, pois corresponde a tomar 3,1605 como valor para 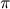 ao invés de 3m14159....
Porém os gregos antigos também tentaram achar outras soluções, através de algumas curvas que foram inventadas, ou através de construções mecânicas.
Anaxágoras foi o primeiro matemático do qual temos registro de ter tentado solucionar este problema.
Dinostratos desenvolveu um método para quadrar o círculo através de quadratriz ou trissectriz de Hipias.
A quadratriz de Hipias consiste em uma curva mecânica, que pode ser obtida da seguinte maneira:
ao invés de 3m14159....
Porém os gregos antigos também tentaram achar outras soluções, através de algumas curvas que foram inventadas, ou através de construções mecânicas.
Anaxágoras foi o primeiro matemático do qual temos registro de ter tentado solucionar este problema.
Dinostratos desenvolveu um método para quadrar o círculo através de quadratriz ou trissectriz de Hipias.
A quadratriz de Hipias consiste em uma curva mecânica, que pode ser obtida da seguinte maneira: