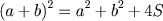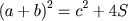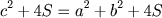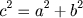O enunciado do teorema, que ficou conhecido como de
Pitágoras, é:
num triângulo retângulo, o quadrado da hipotenusa é igual a soma dos quadrados dos catetos.
Esse resultado já era conhecido pelos
babilônios da época de
Hamurabi, mas atribui-se à Pitágoras sua descoberta, pois supõe-se
que a demonstração formal foi feita por ele.
Não se sabe ao certo o método utilizado por Pitágoras para a demonstração,
supõem-se que foi uma prova por comparação de áreas de figuras geométricas,
como apresentaremos a seguir.
Considere dois quadrados, ambos com lado iguais a
(a + b). O primeiro é
composto por seis figuras: um quadrado de lado
a, um quadrado de lado
b e
quatro triângulos retângulos de catetos
a e
b. Se chamarmos de
S a área de um
desses triângulos e sendo a área total da figura
(a + b)2, temos:
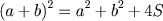
O segundo quadrado é composto também de quatro triângulos retângulos iguais
aos anteriores e de um quadrado de lado c, equivalente à hipotenusa dos
triângulos. Logo, nesse quadrado, temos:
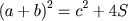
Igualando os segundos membros das equações, resulta:
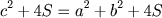
Agora se cancelarmos o termo
4S em ambos os lados da igualdade acima,
resulta expressão central do
Teorema de Pitágoras:
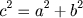
A figura abaixo ilustra esta demonstração.
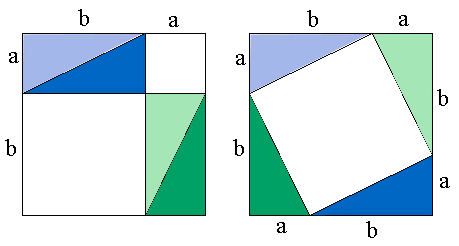
Abaixo a mesma ilustração, desta vez utilizando o programa de Geometria Interativa
iGeom
(precisa de um navegador Web com plugin para Java).
Na contrução interativa do Teorema de Pitágoras com o iGeom,
pode-se clicar sobre os pontos A, B ou E, então solte o botão do "mouse" e mova-o pela tela.
Para carregar uma imagem estática da construção interativa
clique aqui.