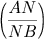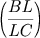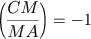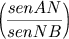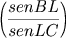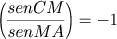As origens da trigonometria são incertas. É possível encontrar problemas que envolvem a co-tangente no
Papiro Rhind e uma notável tábua de secantes na tábua cuneiforme babilônica Plimpton 332.
O desenvolvimento da trigonometria esta bastante ligado à astronomia. Os astrônomos babilônicos dos séculos IV e V a.C. obtiveram várias informações que foram transmitidas para os gregos, foi essa astronomia primitiva que deu origem à trigonometria esférica.
Foram os gregos que pela primeira vez fizeram um estudo das relações entre ângulos (ou arcos) num círculo e os comprimentos que subtendem. Nas obras de Euclides já existiam teoremas equivalentes a leis ou fórmulas trigonométricas. Em
Os elementos é possível encontrar as leis do cosseno para ângulos obtusos e agudos, respectivamente, nas Proposições II.12 e II.13, porém enunciadas em linguagem geométrica.
Hiparco de Nicéia ganhou o direito de ser chamado "o pai da trigonometria" pois na segunda metade do século II a.C., fez um tratado em doze livros que se ocupa da construção do que deve ter sido a primeira tabela trigonométrica, uma tábua de cordas, Ptolomeu também construiu uma tabela de cordas que fornece o seno dos ângulos de
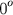
a
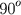
com incrementos de 15". Evidentemente Hiparco fez estes cálculos para usá-los em sua astronomia.
Também parece ter sido Hiparco o primeiro a dividir o círculo em
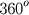
na sua tábua de cordas. Talvez ele tenha tomado a idéia de Hipsicles que dividiu o dia em 360 partes (inspirado na astronomia babilônica).
Teon de Alexandria menciona um tratado de
Cordas num círculo em seis livros, escrito por Menelau de Alexandria, que assim como vários outros de seus tratados se perdeu. Felizmente o seu tratado
Sphaerica, em três livros, se preservou numa versão árabe.
No Livro I estabelece uma base teórica para estudo dos triângulos esféricos
assim como Euclides fez para os triângulos planos, como teoremas usuais de
congruência e teoremas sobre triângulos isósceles entre outros. Além disso,
contém um teorema que não possui um análogo euclidiano, dois triângulos
esféricos são congruentes quando os ângulos correspondentes são iguais
(ele não fazia distinção entre triângulos esféricos congruentes e simétricos).
Estabelece-se também o fato de que a soma dos ângulos de um triângulo esférico
é maior que
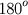
. O Livro II contém teoremas de interesse da astronomia e no
livro III desenvolve-se a trigonometria esférica através da proposição
conhecida como teorema de Menelau: se uma transversal intercepta os lados BC, CA, AB de um triângulo ABC nos pontos L, M, N, respectivamente, então:
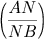
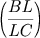
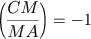
Analogamente na trigonometria esférica ao invés de uma transversal temos um círculo máximo transversal interceptando os lados BC, CA, AB de um triângulo esférico ABC, respectivamente nos pontos L, M, N e a conclusão correspondente é:
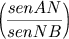
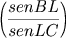
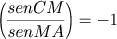
Porém a mais influente e significativa obra trigonométrica da antigüidade foi a
Syntaxis matematica, obra escrita por Ptolomeu que contém 13 livros. Este tratado é famoso por sua compacidade e elegância, e para distinguí-lo de outros foi associado a ele o superlativo
magiste ou "o maior". Mais tarde na Arábia o chamaram
Almagesto, por designação da lingua, e a partir de então a obra é conhecida por esse nome.




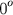 a
a 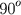 com incrementos de 15". Evidentemente Hiparco fez estes cálculos para usá-los em sua astronomia.
Também parece ter sido Hiparco o primeiro a dividir o círculo em
com incrementos de 15". Evidentemente Hiparco fez estes cálculos para usá-los em sua astronomia.
Também parece ter sido Hiparco o primeiro a dividir o círculo em 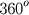 na sua tábua de cordas. Talvez ele tenha tomado a idéia de Hipsicles que dividiu o dia em 360 partes (inspirado na astronomia babilônica).
Teon de Alexandria menciona um tratado de Cordas num círculo em seis livros, escrito por Menelau de Alexandria, que assim como vários outros de seus tratados se perdeu. Felizmente o seu tratado Sphaerica, em três livros, se preservou numa versão árabe.
No Livro I estabelece uma base teórica para estudo dos triângulos esféricos
assim como Euclides fez para os triângulos planos, como teoremas usuais de
congruência e teoremas sobre triângulos isósceles entre outros. Além disso,
contém um teorema que não possui um análogo euclidiano, dois triângulos
esféricos são congruentes quando os ângulos correspondentes são iguais
(ele não fazia distinção entre triângulos esféricos congruentes e simétricos).
Estabelece-se também o fato de que a soma dos ângulos de um triângulo esférico
é maior que
na sua tábua de cordas. Talvez ele tenha tomado a idéia de Hipsicles que dividiu o dia em 360 partes (inspirado na astronomia babilônica).
Teon de Alexandria menciona um tratado de Cordas num círculo em seis livros, escrito por Menelau de Alexandria, que assim como vários outros de seus tratados se perdeu. Felizmente o seu tratado Sphaerica, em três livros, se preservou numa versão árabe.
No Livro I estabelece uma base teórica para estudo dos triângulos esféricos
assim como Euclides fez para os triângulos planos, como teoremas usuais de
congruência e teoremas sobre triângulos isósceles entre outros. Além disso,
contém um teorema que não possui um análogo euclidiano, dois triângulos
esféricos são congruentes quando os ângulos correspondentes são iguais
(ele não fazia distinção entre triângulos esféricos congruentes e simétricos).
Estabelece-se também o fato de que a soma dos ângulos de um triângulo esférico
é maior que 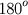 . O Livro II contém teoremas de interesse da astronomia e no
livro III desenvolve-se a trigonometria esférica através da proposição
conhecida como teorema de Menelau: se uma transversal intercepta os lados BC, CA, AB de um triângulo ABC nos pontos L, M, N, respectivamente, então:
. O Livro II contém teoremas de interesse da astronomia e no
livro III desenvolve-se a trigonometria esférica através da proposição
conhecida como teorema de Menelau: se uma transversal intercepta os lados BC, CA, AB de um triângulo ABC nos pontos L, M, N, respectivamente, então: