Voltar
Cada exercício no iComb consiste na determinação do tamanho (cardinalidade) de um conjunto, considerando determinado universo (como as cartas de um baralho). Entretanto o aluno não deve simplesmente digitar um número resposta, mas deve decompor a descrição original do problema em estágios (que resulta em um problema mais simples) e para cada estágio determinar sua cardinalidade.
Após a construção dos estágios o aluno deve determinar como estes devem ser agrupadas para produzir a resposta final. Atualmente para as decomposições (em estágios) aceitas no iComb, os agrupamentos possível são: multiplicar ou somar a cardinalidade de estágios.
Por exemplo, considere o exercício @numeroExerc@ da página de exercícios, cujo enunciado é:
Figura 1: Um conjunto válido de 20 elementos Note que o baralho de 32 cartas é o baralho do pôquer, formado pela retirada de todas as cartas inferiores a 7. Assim as cartas do baralho de 32 cartas são aquelas de valores 7, 8, 9, 10, Valete, Dama, Rei e Ás, com cada um dos 4 naipes (ouros , espadas , copas e paus ) resultando nas 32 cartas.
Abaixo será apresentado uma possível decomposição, que utiliza 4 estágios, que resolver o problema acima:

1. Defina os 4 estágios abaixo
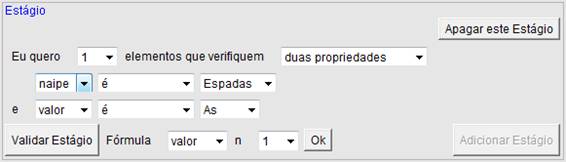
   Figura 2: Primeiro Estágio: 1 elemento tal que naipe é espadas e valor é ás.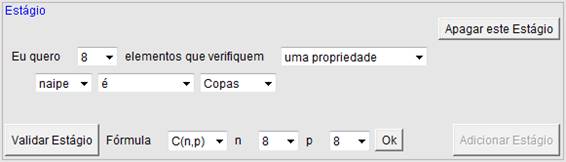
   Figura 3: Segundo Estágio: 8 elementos tal que naipe é copas.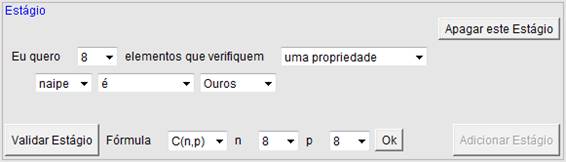
   Figura 4: Terceiro Estágio: 8 elementos tal que naipe é ouros.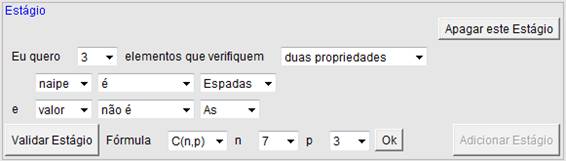
   Figura 5: Quarto Estágio: 3 elementos tal que naipe é espadas e valor não é ás.
2. Selecione multiplicar e depois acione Validar Construção
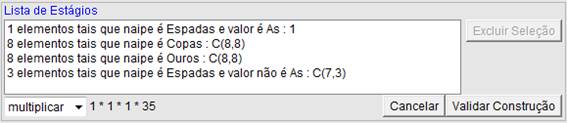
   Figura 6: Lista de Estágios

Solução corretas e Incorretas
Os 4 estágios acima permitem gerar uma solução para o exercício. Porém, outras soluções podem ser criadas para o mesmo exercício. Por exemplo, o conjunto de estágios:

1. 1 elemento tal que o naipe é espadas e o valor é ás
2. 16 elementos tal que o naipe é vermelho
3. 3 elementos tal que o naipe é espadas e o valor não é ás

Também é uma solução para o mesmo exercício. Se o aluno propor qualquer uma destas decomposições o iComb avaliará automaticamente a solução como correta.
Por outro lado, existe uma infinidade de decomposições em estágios que NÃO são podem resultar em solução correta para o problema. Se o aluno propor qualquer uma delas, o iComb avisará ao aluno que esta não é uma solução para o problema proposto, sugerindo que ele tente novamente.
Por exemplo, o conjunto de estágios abaixo sempre resultará em uma solução incorreta:

1. 4 elementos tal que o naipe é espadas
2. 16 elementos tal que o naipe é vermelho

Para entender o porquê desta decomposição resultar sempre em erro, note que é possível selecionar um elemento com que não respeita a restrição de ter 3 áses: o estágio 1 obriga a tomar 4 elementos cujo naipe seja espadas, assim no universo considerado (32 cartas do baralho do pôquer), pode-se pegar os elementos 7, 8, 9 e Valete todos de espadas: , , , . Muitas vezes, a presença de apenas 1 estágio é suficiente para concluirmos que a solução não será alcançada. É o caso do estágio 4 elementos tal que o naipe é espadas. Outro exemplo é o estágio:

1. 3 elementos tal que valor é ás

Note que podemos neste caso selecionar o ás de paus, mas como precisamos de 16 cartas vermelhas e mais 4 cartas de espadas, não há espaços para cartas de paus uma vez que o total de elementos do conjunto deverá ser 20 como diz o enunciado.
Enfim, para resolver exercícios utilizando o iComb certifique-se que:

1. Estágios não se sobreponham: Nenhum elementos poderá ter potencial de ser selecionado por mais do que um estágio. Como exemplo os estágios 1 elemento tal que naipe seja copas e 1 elemento tal que valor seja ás são naturalmente incompatíveis e nunca poderão pertencer a mesma solução. Observe que o Ás de Copas pode ser selecionado pelos dois estágios.
2. Um estágio não inclua elementos não solicitados. É o caso do estágio 3 elementos tal que o valor é ás do exercício acima. Ele pode incluir o elementos ás de paus que é indesejado? no contexo do exercício.
3. Todos os elementos desejados sejam selecionados.