
|
iMática -
Problemas da RPM 44
|

|
Élvia Mureb Sallum
Flávio Wagner Rodrigues
IME-USP
Soluções e Sugestões
RPM - Problemas
Caixa Postal 66281
05315-970 São Paulo, SP
|
Problemas
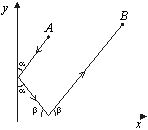
- Dados os pontos A e B no primeiro quadrante, quais as condições sobre suas coordenadas para que exista uma trajetória "tipo bilhar" como a indicada na figura?
(Enviado por Chico Nery, Campinas, SP.) |
|
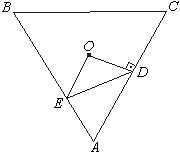
- Na figura ABC é um triângulo equilátero, O é o centro da circunferência inscrita e BE é igual à altura do triângulo. Determinar a área do triângulo ODE em função do lado.
(Enviado por Geraldo Perlino, SP.)
|
|
- Encontre todos os números naturais de dois dígitos tais que sua soma com o número formado pelos mesmos dígitos em ordem contrária resulta um quadrado perfeito.
(Retirado de uma seleção para treinamento para a Olimpíada Soviética de Matemática.)
|
- Um L-treminó é uma figura plana como a do desenho (ou uma rotação dela). Considere um "tabuleiro de xadrez" de tamanho
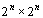 do qual se remove uma qualquer das casas. Mostre que o restante do tabuleiro pode ser coberto por L-treminós sem superposição. do qual se remove uma qualquer das casas. Mostre que o restante do tabuleiro pode ser coberto por L-treminós sem superposição.
(Retirado do livro Problem-solving strategies, de Arthur Engel.)
|
|
- Antônio e Bento, dois gêmeos, seguiam o leito de uma ferrovia
e começaram a atravessar uma ponte estreita na qual havia espaço
apenas para o trem. No momento em que completavam 2/5 do percurso da ponte,
ouviram o trem que se aproximava por trás deles. Antônio começou
a correr de encontro ao trem, saindo da ponte praticamente no instante em
que o trem entrava. Bento correu no sentido oposto a Antônio, conseguindo
sair da ponte praticamente no instante em que o trem saía. Quando os
irmãos se reencontraram, passado o sufoco, o irmão que gostava
de Matemática (o outro amava) observou:
- Corremos
à velocidade de 15 km por hora e portanto já sei
calcular a velocidade do trem!
Calcule a velocidade do trem. Justifique sua resposta!
- Determine o número fantasma de seis algarismos que está escondido
na última linha. Nas outras linhas há também números
de seis algarismos e aolado de cada um deles está anotado
quantos algarismos há em comum com o número fantasma: são
B (bom) se estão colocados na mesma posição
no número fantasma e R (regular) se estão no número
fantasma, mas em posição diferente.
(Extraído do
El Acertijo, número 3, 1992.)
|
|
|
B
|
R
|
|
1 3 5 2 4 6
|
2
|
0
|
|
5 7 9 6 8 0
|
2
|
2
|
|
2 6 0 4 8 1
|
2
|
2
|
|

|
6
|
0
|
|
- Encontre o menor número ABCDEF, formado
pelos algarismos 1, 2, 3, 4, 5 e 6, sem repetição, tal
que o número AB seja divisível por B, o
número BC seja divisível por C, CD
seja divisível por D, DE seja divisível
por E e EF seja divisível por F.
(Extraído do El Acertijo, número 3, 1992.)
|

(Respostas a serem implementadas...)
|


