- Dados dois
pontos A e B do plano e uma constante
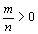 , determinar o lugar geométrico
dos pontos P do plano tais que , determinar o lugar geométrico
dos pontos P do plano tais que 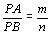
.
1a
Solução:
- Quando
 ,
o lugar geométrico dos pontos P do plano tais que ,
o lugar geométrico dos pontos P do plano tais que 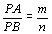 é a mediatriz de AB, pois ( é a mediatriz de AB, pois (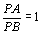 Û P
Î mediatriz de AB).
Û P
Î mediatriz de AB).
- Quando
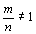 ,
consideraremos, sem perda de generalidade, o caso ,
consideraremos, sem perda de generalidade, o caso 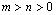
.
|
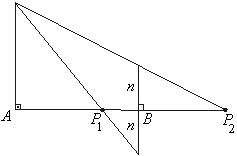
a)
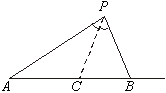
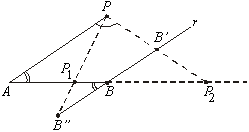
A construção ao lado mostra que existem dois pontos 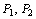 da reta AB tais que da reta AB tais que
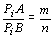 , , 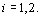
A
verificação se faz através de semelhança de triângulos.
|
|
- Os pontos
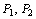 obtidos em a) são os únicos da reta AB tais que obtidos em a) são os únicos da reta AB tais que 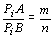 . (Por quê?) . (Por quê?)
- Se P
é um ponto fora da reta AB tal que
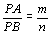 , mostremos que P pertence à
circunferência C que passa por , mostremos que P pertence à
circunferência C que passa por 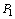 e e 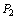 e tem diâmetro e tem diâmetro  . De fato: . De fato:
| Sendo
PC bissetriz interna do ângulo 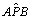 , segue do teorema da bissetriz
interna: , segue do teorema da bissetriz
interna:
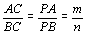 . .
|
|
| Sendo
PD bissetriz externa do ângulo  , segue do teorema da
bissetriz externa: , segue do teorema da
bissetriz externa:
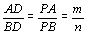 . .
|
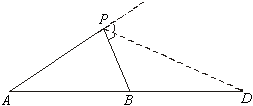
|
Como
C e D são pontos da reta AB tais que 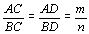 ,
então, por b), ,
então, por b), 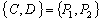 .
(A existência do ponto D é garantida por termos .
(A existência do ponto D é garantida por termos 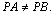 ) )
Logo, P pertence à circunferência
C, já que as bissetrizes interna e externa são perpendiculares.
- Reciprocamente,
dado um ponto P na circunferência C, mostremos que
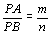
e então concluiremos
que o lugar geométrico dos pontos P é a circunferência C.
Tracemos
por B a reta r paralela a AP. Temos:
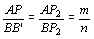 (de (de  ) e ) e 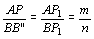 , ,
(de
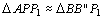 ). ).
| 
|
Logo,
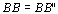 , isto é, PB é mediana do
triângulo retângulo , isto é, PB é mediana do
triângulo retângulo 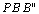 . .
Isso
implica (verifique!)
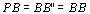 e, portanto, e, portanto,
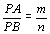 . .
|
Observação: o raio da circunferência
C é 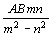 , obtido de: , obtido de:
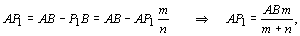
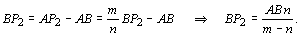
(Adaptada
das soluções enviadas por Antonio Ferreira Sobrinho e outros
leitores.)
2a Solução:
O problema é clássico em Geometria Analítica, com a solução:
Se
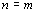 , obtemos a mediatriz; se , obtemos a mediatriz; se 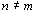 , obtemos a circunferência. , obtemos a circunferência.
- Se dois triângulos
têm dois ângulos respectivamente iguais e dois ângulos respectivamente
suplementares, mostre que os lados opostos aos ângulos iguais
são proporcionais aos lados opostos aos ângulos suplementares.
Solução:
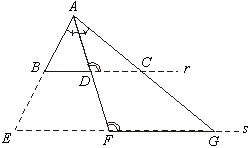
Os
triângulos do enunciado podem ser considerados justapostos como
ABD e AFG da figura.
| 
|
Queremos
mostrar que 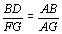 . Aplicando o teorema da bissetriz
interna ao triângulo ABC, temos . Aplicando o teorema da bissetriz
interna ao triângulo ABC, temos 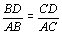 . .
Como
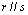 , temos , temos 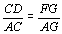 . .
Logo,
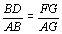 . .
|
(Solução
enviada por João Linneu do Amaral Prado, SP.)
- Dez times,
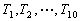 , participam de um campeonato no qual cada time joga com todos os outros
uma única vez. Os 45 jogos serão realizados em 9 rodadas, cada
uma com 5 jogos. Construa uma tabela para esse campeonato, ressaltando,
se for o caso, aspectos geométricos de sua solução. , participam de um campeonato no qual cada time joga com todos os outros
uma única vez. Os 45 jogos serão realizados em 9 rodadas, cada
uma com 5 jogos. Construa uma tabela para esse campeonato, ressaltando,
se for o caso, aspectos geométricos de sua solução.
Solução:
Inicialmente
vamos deixar 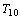 de fora e construir uma tabela para
os 36 jogos que envolvem os times de fora e construir uma tabela para
os 36 jogos que envolvem os times 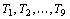 . É claro que cada rodada terá quatro
jogos e um dos times irá necessariamente ficar fora. Se o nosso
processo de construção fizer com que cada um dos nove times
fique fora uma e uma só vez, a tabela será completada colocando
o quinto jogo de cada rodada entre o time que ficou fora e . É claro que cada rodada terá quatro
jogos e um dos times irá necessariamente ficar fora. Se o nosso
processo de construção fizer com que cada um dos nove times
fique fora uma e uma só vez, a tabela será completada colocando
o quinto jogo de cada rodada entre o time que ficou fora e 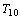 . Na proposta que faremos a seguir,
vamos convencionar que . Na proposta que faremos a seguir,
vamos convencionar que 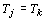 se j for congruente a k módulo
9. se j for congruente a k módulo
9.
Para
a i-ésima rodada 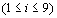 , os jogos serão: , os jogos serão:
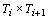 ; ; 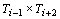 ; ; 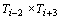 ; ; 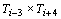 , ficando fora , ficando fora  . .
Em
palavras, 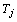 enfrenta enfrenta 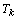 na i-ésima rodada se e só se na i-ésima rodada se e só se
 for congruente
a for congruente
a 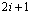 módulo 9. Esquematizando: módulo 9. Esquematizando:
| 
|

|

|
| 1a
rodada, fica fora 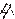 |
2a
rodada, fica fora 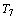 |
3a
rodada, fica fora 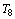 |
A
sétima rodada, por exemplo, será constituída pelos jogos:
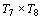 ; ; 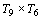 ; ; 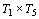 ; ; 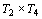 . .
A
soma dos índices será congruente a  . .
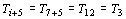 fica fora nessa rodada. fica fora nessa rodada.
Com
essa construção fica fácil mostrar que os times se enfrentam
uma e uma só vez e que nenhum time é escalado para mais de um
jogo numa mesma rodada. Finalmente, cada um dos nove times fica
fora uma e uma só vez, permitindo que a tabela seja completada.
- Os números
inteiros
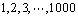 são escritos em ordem em volta de um círculo. A partir do número 1,
marque todo décimo quarto número, isto é, marque são escritos em ordem em volta de um círculo. A partir do número 1,
marque todo décimo quarto número, isto é, marque 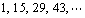
, parando no
momento em que for atingido um número já marcado. Determine quantos
números não marcados restam.
Solução:
Na
primeira etapa serão marcados os números 1, 15, 29, ..., isto é,
todos os números menores do que 1000 que divididos por 14 deixam
resto 1. O último número desse conjunto é 995, o que nos permite
concluir que na segunda etapa serão marcados todos os números que
divididos por 14 deixam resto 9. Um raciocínio análogo nos permite
determinar o que ocorre nas etapas seguintes.
| Etapa |
Começa
com |
Termina
em |
| 2a |
9 |
989 |
| 3a |
3 |
997 |
| 4a |
11 |
991 |
| 5a |
5 |
999 |
| 6a |
13 |
993 |
| 7a |
7 |
987 |
É
fácil ver que a próxima etapa começaria com o número 1, repetindo
assim a primeira, o que nos permite concluir que o processo termina
após sete etapas. Para determinar a quantidade de números não marcados,
a maneira direta seria somar os números de termos de cada uma das
progressões aritméticas acima e subtrair o total de 1000. O mais
simples é observar que qualquer número ímpar dividido por 14 deixa
resto ímpar e, portanto, estará incluído em uma das progressões.
Nenhum número par dividido por 14 deixa resto ímpar e, portanto,
existem exatamente 500 números não marcados.
Relação
dos leitores que enviaram soluções dos
problemas
da RPM 40
| Alberto
H. Raad, MG – 170, 171,172, 173 |
José
Hernandez, SP – 171
|
|
André
Luis Souza de Araujo, RJ – 170
|
Luciano
Marinho Filho, PE – 171, 172, 173
|
|
André
L. A. Marques, RJ – 170, 172, 173
|
Lusmilla
M. F. Santos, RR – 173
|
|
Angelo
Papa Neto, CE – 171, 173
|
Marcos
Luiz Henrique, PE – 171, 172, 173
|
|
Antonio
Ferreira Sobrinho, SP – 170
|
Marisa
Moreni Lopes, SP – 171
|
|
Carlos
A. S. Victor, RJ – 170, 171,172,173
|
Mauricio
T. Oliveira, SP – 171, 172, 173 |
|
Davi
Máximo A. Nogueira, CE – 171
|
Noisés
Pereira da Silva, PE – 172
|
|
Celso
Martinez Rodrigues, MG – 171, 173
|
Roberto
L. Spenthof, PR – 170, 171, 172, 173
|
|
F.
W. Leão, RJ – 170, 172
|
Roberto
Luiz Dotto, SP – 172, 173
|
|
Francisco
A. M. Paiva, CE – 170, 171
|
Ruy
Carlos Miritz, RS – 171,173
|
|
Fernando
Carvalho Ramos, RS – 173
|
Sebastião
Paulo Tonolli, SP – 171, 172, 173
|
|
Giancarlo
Miragliotta, SP – 170, 171
|
Sigridi
de Almeida Borges, SP – 171
|
|
J.
Claudio M. Velloso, RJ – 170, 173
|
Sun
Hsien Ming, SP – 173
|
|
Janilson
A. Balieri, MG – 173
|
Tsunediro
Takahaski, SP – 170, 171
|
|
João
Linneu do A. Prado, SP – 170, 171
|
Wanderlei
Gamba, SP – 171, 173
|
|
Joaquim
Ferreira da Silva, PE – 173
|
Wellington
R. de Assis, RJ – 170, 171, 173
|
|
Jorge
Ferreira dos Santos, RJ – 171
|
|
Nota: O leitor Wanderley Gamba, SP, nos
enviou uma solução correta do problema 167, e o leitor Manuel
João de Jesus Almeida, RJ, nos enviou uma solução correta
do problema 165. Por falha nossa, seus nomes não saíram na lista
dos acertadores da RPM 41. A eles nossas sinceras desculpas.
-
|


