
|
iMática -
Soluções dos Problemas propostos na: RPM 42
|
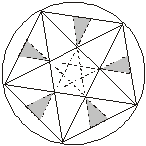
- A figura ao lado mostra um pentágono
regular inscrito numa circunferência de raio unitário. Determine a
medida da área sombreada.
|
|
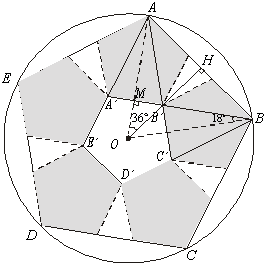
Solução:
|
|
Sendo
o raio da circunferência unitário, temos:
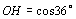
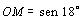
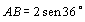
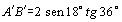 . .
Então,
área OAB 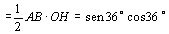 . .
|
E área 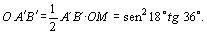
Se S= área 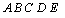 e s= área e s= área 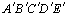 , então , então
S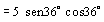 e
s e
s 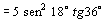 . .
Logo, a área
A procurada é dada por
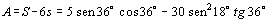 . Substituindo os valores . Substituindo os valores
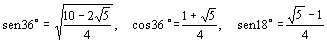 (ver RPM 36), obtemos (ver RPM 36), obtemos 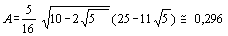 . .
(Adaptada
da solução enviada por Geraldo Perlino, SP.)
- Sejam a,
b, c retas paralelas distintas duas a duas. Mostre
que existem triângulos equiláteros cujos vértices A, B,
C são pontos das retas a, b, c respectivamente.
Solução:
Considere
a, b, c retas paralelas coplanares.
A
seguinte construção pode ser feita usando apenas régua e compasso.
Fixamos
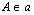 e fazemos uma rotação de e fazemos uma rotação de 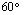 , no sentido anti-horário, da
reta b em torno de A, obtendo uma reta , no sentido anti-horário, da
reta b em torno de A, obtendo uma reta 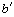 que
corta a reta c no ponto C. que
corta a reta c no ponto C.
| 
ou
|
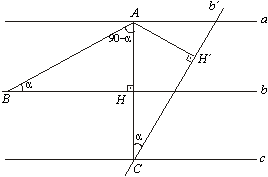 |
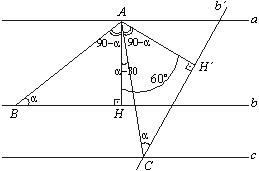
Fazemos
a rotação, no sentido horário, do ponto C em torno de A,
obtendo na interseção com b o ponto 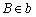 . .
Os
triângulos retângulos AHC e 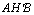 são congruentes, uma vez que são congruentes, uma vez que
AH
= 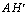 e AB = AC. Logo, e AB = AC. Logo, 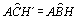 = =
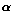 , que implica , que implica 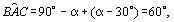 de modo que o de modo que o  ABC é equilátero. ABC é equilátero.
(Solução
enviada por F. W. Leão, RJ.)
Obs.:
O leitor Alberto Hassen Raad, MG, observou
e provou, usando Geometria Analítica, que o enunciado também vale
se as retas a, b e c são paralelas não coplanares.
- Use um argumento
combinatório para determinar o valor de
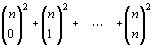
sendo
n um inteiro maior ou igual a 1.
Solução:
Um
grupo de 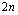 pessoas é formado por n homens
e n mulheres. Existem pessoas é formado por n homens
e n mulheres. Existem 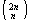 maneiras de escolhermos um conjunto de
n pessoas desse grupo. Vamos determinar em quantos desses
conjuntos existem exatamente K homens. Para isso vamos observar
que os K homens podem ser escolhidos de maneiras de escolhermos um conjunto de
n pessoas desse grupo. Vamos determinar em quantos desses
conjuntos existem exatamente K homens. Para isso vamos observar
que os K homens podem ser escolhidos de 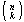 maneiras e as n-k mulheres de maneiras e as n-k mulheres de 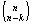 maneiras. Segue-se que, para maneiras. Segue-se que, para 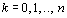 , o número de conjuntos de n pessoas
que contêm exatamente K homens será dado por , o número de conjuntos de n pessoas
que contêm exatamente K homens será dado por 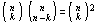 . .
Conclui-se
portanto que 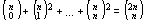
(Adaptada
da solução enviada por Carlos A. Gomes da Silva, RN.)
Nota:
Vários leitores determinaram o valor da expressão utilizando indução,
desenvolvimento de binômios, etc. Essas soluções não foram consideradas
porque a questão pedia explicitamente a utilização de um argumento
combinatório.
- Mostre que,
se n é um número inteiro, positivo, ímpar e não primo,
então n pode ser expresso como uma soma de três ou mais
números inteiros, positivos e consecutivos. Essa representação
é única?
Solução:
Como
n é ímpar e não é primo, n pode ser expresso como
um produto 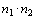 , onde , onde 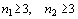 e e 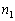 e e 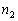 são
ambos ímpares. Vamos supor, sem perda de generalidade, que são
ambos ímpares. Vamos supor, sem perda de generalidade, que 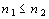 . Como . Como 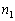 é ímpar, nós podemos considerar a seqüência
de é ímpar, nós podemos considerar a seqüência
de 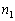 números consecutivos que tem números consecutivos que tem 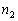 como
termo central. O número de termos dessa seqüência é maior ou igual
a 3 e a soma deles é igual a como
termo central. O número de termos dessa seqüência é maior ou igual
a 3 e a soma deles é igual a 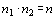 .
Da hipótese .
Da hipótese 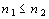 segue-se que todos os termos da seqüência são positivos. Por outro lado,
é fácil mostrar que a representação não é única. Por exemplo, segue-se que todos os termos da seqüência são positivos. Por outro lado,
é fácil mostrar que a representação não é única. Por exemplo, 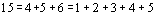 . O leitor interessado poderá
tentar encontrar condições que n deve satisfazer para que
a representação seja única. . O leitor interessado poderá
tentar encontrar condições que n deve satisfazer para que
a representação seja única.
Relação
dos leitores que enviaram soluções dos
problemas
da RPM 42
| |
|
|
Alberto Hasser Raad, MG –
178, 179
|
Guita Nascimento, RJ – 178
|
|
Amadeu Carneiro de Almeida,
RJ – 178, 179
|
João Linneu do A. Prado, SP
– 178, 181
|
|
Américo Antônio Figo, SP –
179
|
Jorge Ferreira dos Santos,
RJ – 178
|
|
André Luiz S. de Araújo, RJ
– 179, 181
|
Luciano Marinho Filho, PE
– 178
|
|
Antonio Ferreira Sobrinho,
SP – 178
|
Marcos Garcia de Souza, SP
– 181
|
|
Carlos A. da Silva Victor,
RJ – 179, 181
|
Milton Dini Maciel, SP – 178
|
|
Carlos A. Gomes da Silva,
RN – 180
|
Ricardo Klein Hoffmann, RS
– 180
|
|
Cristovam A. Girodo, SP –
178
|
Roberto Luis Dotto, SP – 178
|
|
Ercole Pellicano Neto, SP
– 180
|
Trajano Pires da Nóbrega Neto,
SP – 181
|
|
F. W. Leão, RJ – 178, 179,
180, 181
|
Tsunediro Takahaski, SP –
179
|
|
Fernando Carvalho Ramos, RS
– 178,181
|
Wanderley Gamba, SP – 178,
181
|
|
Geraldo Perlino, SP – 178
|
Zilton Gonçalves, RJ – 178
|
|
Geraldo Perlino Junior, SP
– 179, 181
|
|
NOTA:
Recebemos, com tristeza, a notícia do
falecimento (agosto/00) de nosso leitor Francisco Wilson Leão
que durante 13 anos, sem interrupção, constou da lista de acertadores
desta seção como F. W. Leão, RJ. Enviou-nos, pouco antes
de falecer, a carta com os quatro problemas da RPM 42 resolvidos
corretamente.
Obs.
Na relação de acertadores publicada na RPM 42 foi omitido
o recebimento da solução correta do problema 171 enviada por André
Souza de Araújo. A ele nossas desculpas.
|
|


