Arthur Cayley nasceu em 16 de agosto de 1821 em Richmond na Inglaterra. Vindo de uma família de comerciantes, seu pai desejava que continuasse os negócios da família, porém em 1835 ingressou no King´s College School onde sua aptidão para a matemática se tornou mais aparente, assim seu pai resolveu envia-lo para Cambridge.

Em 1838 começou seus estudos no Trinity College em Cambridge onde se graduou em 1842.

Em 1843 trabalhou fundamentalmente em álgebra, mas, também trabalhou em geometrias não-euclideanas e geometria n-dimensional, usando determinantes como elemento essencial.

A partir de 1849 trabalhou catorze anos como advogado, ele desistiu da docência, pois continuar nela implicaria em tomar hábitos religiosos. Embora muito hábil nessa carreira, a considerava apenas como uma forma de sustento para prosseguir com a matemática. Durante esses catorze anos publicou aproximadamente 250 trabalhos matemáticos, a maioria sobre a teoria dos invariantes algébricos.

Durante a conferencia de Hamilton sobre os Quatérnios que foi assistir em Dublin, conheceu Salmon, com quem trocou idéias matemáticas por muitos anos. Outro amigo era Sylvester, um advogado com quem trabalhava junto e durante os dias de trabalho conversavam sobre matemática. Ele é considerado, junto com Sylvester, o fundador da teoria dos invariantes.

Foi um dos primeiros matemáticos a estudar matrizes, definindo a idéia de operarmos as matrizes como na álgebra. Descobriu a álgebra das matrizes em 1857. As matrizes surgiram para Cayley ligadas as transformações lineares do tipo:

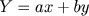
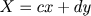
Onde a, b, c, d são números reais, e que podem ser imaginados como aplicações que levam o ponto (x,y) no ponto (X,Y) .

Quando se criou em Cambridge, em 1863 a cadeira sadleriana, está lhe foi oferecida. Assim Cayley aceitou regê-la abandonando a carreira da lei. Tornando-se professor de matemática pura em Cambridge.

Em 1881 foi convidado a dar um curso sobre funções abelianas e funções teta, na Johns Hopkins University nos EUA, onde seu amigo Sylvester era professor.

Cayley ocupa o terceiro lugar entre os escritores de matemática mais prolíferos em toda história desta ciência, perdendo apenas para Euler e Cauchy. Em Collected Mathematical Papers de Cayley há 966 artigos, num total de treze volumes com cerca de 600 páginas cada um, abordando todas as áreas da matemática. Foi neste que Cayley deu construções pioneiras à geometria analítica, teoria das transformações, teoria das curvas e superfícies, o estudo de formas binárias e ternárias.

Charles Hermite registrou as seguintes palavras “talento de Cayley se caracterizou pela clareza e extrama elegância da forma analítica; reforçando por uma capacidade incomparável de trabalho...”