As Cônicas, foram estudadas por Menecmo,
Euclides e
Arquimedes.
A
elipse, a
parábola, a
hipérbole e a
circunferência eram obtidas como
secções de cones circulares retos com planos perpendiculares a um dos elementos do cone,
conforme variação do ângulo no vértice (agudo, reto ou obtuso).
Menecmo descobriu a elipse pesquisando sobre a parábola e a hipérbole, pois ofereciam as propriedades necessárias para a
solução da
duplicação do cubo. Também era de seu conhecimento as equações das curvas conforme a sua
secção: quando formada por secção de um cone circular retângulo era
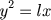
(
l uma constante),
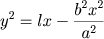
quando secção de cone acutângulo e
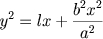
quando secção de
cone obtusângulo. O tratado sobre as cônicas estavam entre algumas das mais importantes obras de Euclides, porém se perderam,
talvez porque logo foram superadas pelo trabalho mais extenso escrito por
Apolônio.
A obra de nível mais avançado foi precisamente a feita por Apolônio de Perga, que substituiu qualquer estudo anterior.
O tratado sobre as Cônicas certamente foi a obra-prima de Apolônio e teve grande influência no desenvolvimento da matemática.
Devido fundamentalmente a este estudo sobre as cônicas ele era conhecido como o
Geômetra Magno.
O tratado consistia em oito livros que contém 387 proposições separadas.
[Heath, 1921] diz que o texto sobre as cônicas é um grande clássico e que merecia ser mais conhecido, porém sua forma
original é muito extensa.
Apenas os quatro primeiros livros foram preservados em grego e felizmente os três seguintes tinham sido traduzidos para árabe e também se preservaram.
Os quatro livros iniciais foram escritos como uma introdução elementar incluindo as proposições básicas das cônicas. A maioria dos resultados destes livros já eram sabidas por Euclides, Aristaeus e outros, como o próprio Apolônio afirmou. Os quatro últimos livros são extensões do assunto, estudos mais avançados.
No Livro 1 se estudam as propriedades dos diâmetros e tangentes das cônicas. No Livro 2 se investigam as relações entre as hipérboles e suas assíntotas. Também se estuda como desenhar tangentes às cônicas dadas. O Livro 3 é o que contém maior número de resultados novos que Apolônio considera os mais belos possíveis.
Os Livros de 5 a 7 são altamente originais. Neles se estuda o problema de achar normais às cônicas e se obtém proposições que determinam o centro de curvatura, o que conduz à equação cartesiana de evoluta. Heath diz que o Livro 5 é o mais notável dos livros existentes.
Foi Apolônio quem pela primeira vez mostrou que a partir de um único cone é possível obter as três espécies de secções cônicas, apenas variando a inclinação do plano de secção. Também provou que o cone não precisa ser reto. Finalmente substituiu o cone de uma só folha por um cone duplo, sendo assim o primeiro a reconhecer a existência dos dois ramos da hipérbole.
Também foi
Cayley quem introduziu os nomes
parábola,
elipse e
hipérbole, utilizados até hoje para identificar as cônicas correspondentes.




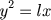 (l uma constante),
(l uma constante),
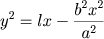 quando secção de cone acutângulo e
quando secção de cone acutângulo e 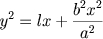 quando secção de
cone obtusângulo. O tratado sobre as cônicas estavam entre algumas das mais importantes obras de Euclides, porém se perderam,
talvez porque logo foram superadas pelo trabalho mais extenso escrito por Apolônio.
A obra de nível mais avançado foi precisamente a feita por Apolônio de Perga, que substituiu qualquer estudo anterior.
O tratado sobre as Cônicas certamente foi a obra-prima de Apolônio e teve grande influência no desenvolvimento da matemática.
Devido fundamentalmente a este estudo sobre as cônicas ele era conhecido como o Geômetra Magno.
O tratado consistia em oito livros que contém 387 proposições separadas.
[Heath, 1921] diz que o texto sobre as cônicas é um grande clássico e que merecia ser mais conhecido, porém sua forma
original é muito extensa.
Apenas os quatro primeiros livros foram preservados em grego e felizmente os três seguintes tinham sido traduzidos para árabe e também se preservaram.
Os quatro livros iniciais foram escritos como uma introdução elementar incluindo as proposições básicas das cônicas. A maioria dos resultados destes livros já eram sabidas por Euclides, Aristaeus e outros, como o próprio Apolônio afirmou. Os quatro últimos livros são extensões do assunto, estudos mais avançados.
No Livro 1 se estudam as propriedades dos diâmetros e tangentes das cônicas. No Livro 2 se investigam as relações entre as hipérboles e suas assíntotas. Também se estuda como desenhar tangentes às cônicas dadas. O Livro 3 é o que contém maior número de resultados novos que Apolônio considera os mais belos possíveis.
Os Livros de 5 a 7 são altamente originais. Neles se estuda o problema de achar normais às cônicas e se obtém proposições que determinam o centro de curvatura, o que conduz à equação cartesiana de evoluta. Heath diz que o Livro 5 é o mais notável dos livros existentes.
Foi Apolônio quem pela primeira vez mostrou que a partir de um único cone é possível obter as três espécies de secções cônicas, apenas variando a inclinação do plano de secção. Também provou que o cone não precisa ser reto. Finalmente substituiu o cone de uma só folha por um cone duplo, sendo assim o primeiro a reconhecer a existência dos dois ramos da hipérbole.
Também foi Cayley quem introduziu os nomes parábola, elipse e hipérbole, utilizados até hoje para identificar as cônicas correspondentes.
quando secção de
cone obtusângulo. O tratado sobre as cônicas estavam entre algumas das mais importantes obras de Euclides, porém se perderam,
talvez porque logo foram superadas pelo trabalho mais extenso escrito por Apolônio.
A obra de nível mais avançado foi precisamente a feita por Apolônio de Perga, que substituiu qualquer estudo anterior.
O tratado sobre as Cônicas certamente foi a obra-prima de Apolônio e teve grande influência no desenvolvimento da matemática.
Devido fundamentalmente a este estudo sobre as cônicas ele era conhecido como o Geômetra Magno.
O tratado consistia em oito livros que contém 387 proposições separadas.
[Heath, 1921] diz que o texto sobre as cônicas é um grande clássico e que merecia ser mais conhecido, porém sua forma
original é muito extensa.
Apenas os quatro primeiros livros foram preservados em grego e felizmente os três seguintes tinham sido traduzidos para árabe e também se preservaram.
Os quatro livros iniciais foram escritos como uma introdução elementar incluindo as proposições básicas das cônicas. A maioria dos resultados destes livros já eram sabidas por Euclides, Aristaeus e outros, como o próprio Apolônio afirmou. Os quatro últimos livros são extensões do assunto, estudos mais avançados.
No Livro 1 se estudam as propriedades dos diâmetros e tangentes das cônicas. No Livro 2 se investigam as relações entre as hipérboles e suas assíntotas. Também se estuda como desenhar tangentes às cônicas dadas. O Livro 3 é o que contém maior número de resultados novos que Apolônio considera os mais belos possíveis.
Os Livros de 5 a 7 são altamente originais. Neles se estuda o problema de achar normais às cônicas e se obtém proposições que determinam o centro de curvatura, o que conduz à equação cartesiana de evoluta. Heath diz que o Livro 5 é o mais notável dos livros existentes.
Foi Apolônio quem pela primeira vez mostrou que a partir de um único cone é possível obter as três espécies de secções cônicas, apenas variando a inclinação do plano de secção. Também provou que o cone não precisa ser reto. Finalmente substituiu o cone de uma só folha por um cone duplo, sendo assim o primeiro a reconhecer a existência dos dois ramos da hipérbole.
Também foi Cayley quem introduziu os nomes parábola, elipse e hipérbole, utilizados até hoje para identificar as cônicas correspondentes.